Sports Betting Strategies
Author: Mishael Roy
Introduction
During this past year, I’ve found myself searching for alpha in emerging markets as a precursor to applying these same techniques in more formal and complex markets. This led me to looking at the world of sports betting, as it fits the criteria for a burgeoning market.
The graph below showcases the legality of sports betting within the 50 states. This graph is updated until the beginning of last year, and the current data will show that sports betting is legal in even more states.
In addition to new legality, a commensurate increase in popularity in sports betting is present. With an increase in legality, number of players, and amount of money transacted, the sportsbooks themselves are learning to set correct odds and prices for players to transact at, in an effort to obtain a recurring profit.
With any developing market, there will be rampant inefficiencies. With odds being determined by betting flow (i.e. the number of players betting and the amount of $$ betted), and the relative lack of sophistication of the average sports bettor, there are ample opportunities for picking off stale odds. To further drive home this point, only around 3% of sports betting accounts end up generating a long-run profit, so 97% of players are then betting likely on “gut-feeling”, which, when compounded among a large number of bettors, results in odds not representing true probabilities, and thus possibly presenting an advantageous transaction point mathematically.
My specific project aimed to take advantage of this with a concrete hypothesis in mind. After many failed attempts to generate anything of meaning, an idea stemmed out of relating identical events in more efficient markets to these newly created American markets, and determining some notion of expected value of the random variable associated with our expected profit on each transaction.
To briefly go into why this would work, it’s important to understand that each sportsbook (FanDuel, DraftKings, etc.) sets their odds independently of one another. This is the same as having the same share of MSFT listed at different prices on different exchanges. At least one of those prices must therefore be wrong, and this can present an opportunity for somebody like myself. If, based on the rules I’ve set out in my code, the random variable associated with the profit we expect to make on a specific transaction is positive over a certain threshold, I bet it. That is, if I expect to make money in the long-term on a specific bet, based on the rules I’ve set, I place the bet. It’s also worth noting that not every bet is equal, pricing for each specific bet is based on a fractional Kelly Criterion approach, more information on that idea can be found here.
Strategy Analysis
Due to this being a currently traded strategy, I’ll further analyze the profitability of this strategy to show that it in fact works and makes some sense to continue pursuing.
Above is the depiction of our realized profit on our strategy over the past 252 days. The Sharpe on these returns is actually relatively low at 0.687. The low Sharpe here can be due to the variance in these returns. Although the returns are very positive in nature, the variability is also extremely high, which will always negatively impact your Sharpe. It’s also worth noting that there was little to no profit during the first half of this graph. This is because of the lack of sporting events and trading opportunities present during the summer months. You’ll see that the latter half of this graph actually coincides with the beginning of the NFL, NBA, and NHL seasons and has really shown how the strategy can perform. With an overall probability of winning money on any specific day ~57% and a daily ROI of ~5%, we still see this as worthwhile to trade, and look deeper into daily return data below.
Below we depict the relationships between the number of bets per day and our day’s P/L, and the number of bets per day and the day’s ROI. These are two key relationships, because they let us know if there is an advantage to each bet we place (i.e. that our strategy works better the more you trade it).
The regression line depicted in both of these charts is positive, which is extraordinarily encouraging in terms of our strategy. Put simply, the more bets we place, the more we expect to win, and the more we expect to win in relation to our total wagered amount. What’s also important is the idea that this strategy is sport-agnostic, so this graph shows that we can bet on whatever odds we want on these sportsbooks, and still make money, because our edge focuses on the principles behind the pricing of these odds, not the sports that these odds actually represent.
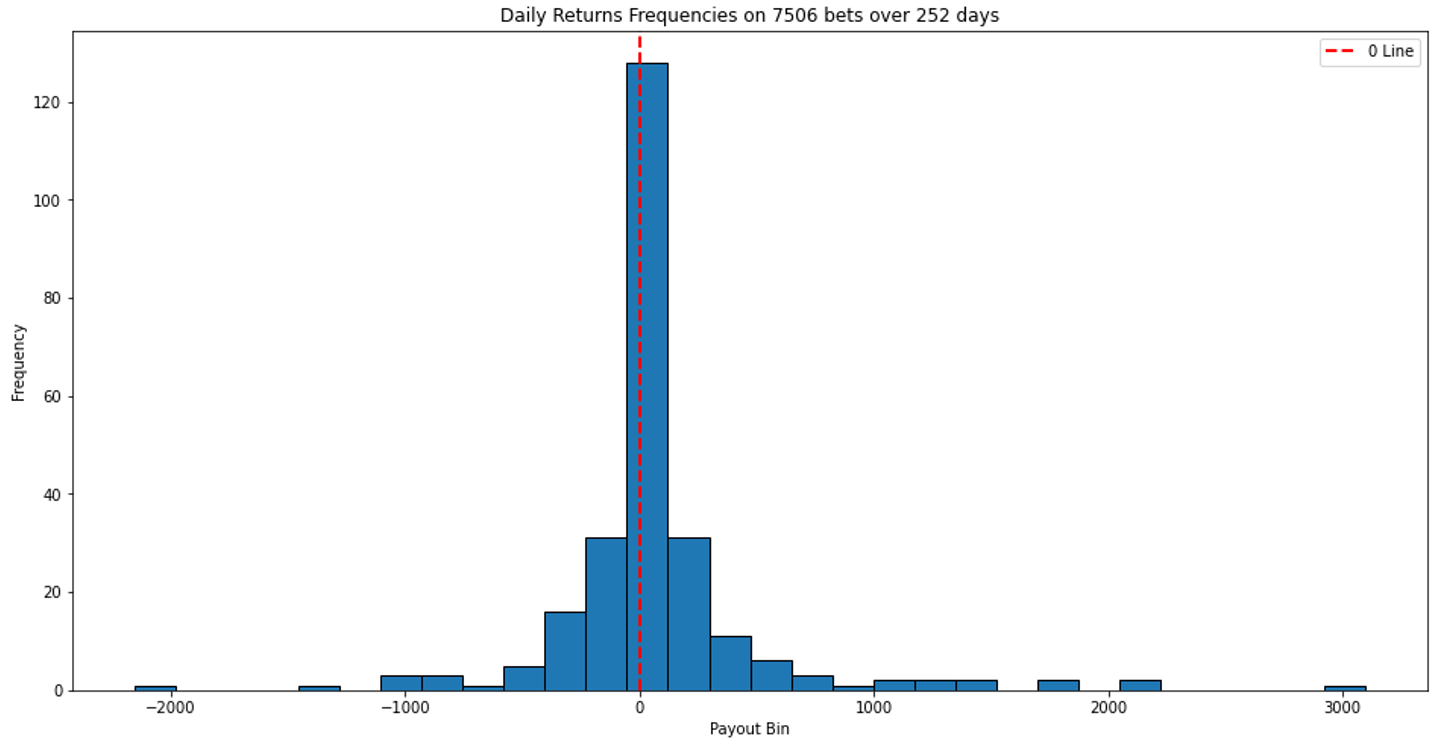
Lastly, we look at normality of our daily returns to determine of the behavior is “nice” to a certain degree. It’s well known that financial returns are normal with fat tails, and we see some similarity here too.
Much of the outlying behavior in our daily return frequencies also occur due to our consistent reinvestment of our earnings. Our histogram also shows relatively high kurtosis metrics which give further credence to the whole “fat-tails” claim.
Final Takeaways
In terms of going forward, profits will be more and more difficult to come by in the coming months, due to many sportsbooks now limiting trades from our accounts because we have won a lot already. Additionally, this strategy is a (somewhat) effortful process, I personally trade on average 30 bets every single day, however I’ve written code that analyzes each odd on each sportsbook to tell me where exactly to look to place a trade. Closer inspection should also be done to further determine if our edge is equally as large on all sporting outcomes (i.e. expected profit on NBA v. NFL bets). In any event, this project has been a quality learning experience in terms of going from hypothesis to connecting data sources to actually taking on risk (which was the most challenging aspect of this project by far) to further analyzing risk and ultimately gaining some notion of consistent profit.